This post is presented as an appendix for my investigation report of Compound Bad Debts. I'll illustrate time-weighted average price(TWAP) conceptually(it's really simple), then the implementation details in Uniswap v3, at last an example and the code will be provided.
Uniswap[1] is a protocol for automated token exchange on many public blockchains. The exchange rate of token0 over token1 is actually the price of token1 in the measurement of token0, if token0 is a stable coin, for instance USDC, then that's our familiar price in U.S dollar.
So Uniswap is not only an decentralized exchange but also a price oracle that provide price information of tokens. Under some conditions(good liquidity pool, active arbitrage,time-weighted average strategy, etc.), that price will be reliable.
In theory, time-weighted average price is easy to understand and compute. I'll illustrate it by an example. Let's assume, at the beginning, uniswap give some price information as follows:
| time range | duration(seconds) | price |
|---|---|---|
| 00:00:00 to 00:00:01 | 1 | p1 |
| 00:00:01 to 00:00:02 | 1 | p2 |
(p1 + p2) / 2
(p1*p2)1/2, namely square root of p1*p2
As time goes on
| time range | duration(seconds) | price |
|---|---|---|
| 00:00:00 to 00:00:01 | 1 | p1 |
| 00:00:01 to 00:00:02 | 1 | p2 |
| 00:00:02 to 00:00:03 | 1 | p3 |
(p1 + p2 + p3) / 3
(p1*p2*p3)1/3, namely cube root of p1*p2
time goes on, but price remain unchanged
| time range | duration(seconds) | price |
|---|---|---|
| 00:00:00 to 00:00:01 | 1 | p1 |
| 00:00:01 to 00:00:02 | 1 | p2 |
| 00:00:02 to 00:00:03 | 1 | p3 |
| 00:00:03 to 00:00:04 | 1 | p3 |
| 00:00:04 to 00:00:05 | 1 | p3 |
we use the same formula to compute mean prices
(p1 + p2 + p3 + p3 + p3) / 5
(p1*p2*p3*p3*p3)1/5
or merge the p3 price from 00:00:02 to 00:00:05
(p1 + p2 + 3*p3) / 5
(p1*p2*p33)1/5
So that's the idea of time-weighted, if a price stayed longer, it contributes more to the final average price. Although arithmetic mean is more intuitive, geometric mean is also reasonable and it's used in Uniswap v3.
The time-weighted average price implementation on Uniswap v3 is closely related to logarithmic price.
That's because the space of possible prices on Uniswap v3 is demarcated by
discrete ticks to facilitate custom liquidity provision. The price at tick i
is given by p=(1.0001)i, then the logarithmic price is represented
as the integer i.
In the other words, the possible prices on Uniswap is an integer power of 1.0001, then the logarithmic price is an integer that can be stored in smaller number of bits.
If logarithmic price is denoted by q, then p1=1.0001q1, p2=1.0001q2,
p3=1.0001q1 the geometric mean prices in the logarithmic price can be
written as:
Look at q1+q2+3*q3, its form is very similar to arithmetic mean. That's the
so-called price accumulator on Uniswap and stored on the blockchain that
anyone can query it to obtain the time-weighted average price.
The price accumulator at time t is defined as the sum of logarithmic price for
basis 1.0001 at every second until time t:
The time-weighted geometric average price over any period t1 to t2 can be evaluated from the price accumulator:
$$ \begin{align*} twap &=1.0001^{\frac{q_{t1} + q_{t1+1} + ... + q_{t2}}{t2-t1}}\\ &=1.0001^{\frac{a_{t2}-a_{t1}}{t2-t1}} \end{align*} $$In practice, the price accumulator is only updated when price changes caused by the token swap.
There some price manipulation discussions in the Uniswap v2 white paper, although some of which don't apply to Uniswap v3 any more, however trade off about choosing appropriate period of time is the same:
Users of the oracle can choose when to start and end this period. Choosing a longer period makes it more expensive for an attacker to manipulate the TWAP, although it results in a less up-to-date price.
The price accumulator information is stored in the UniswapV3Pool[3] Smart
Contract, the state name is observations, the state an array of Oracle.Observation
structure and is public, we can access it through getter function defined in
IUniswapV3PoolState.sol
function observations(uint256 index)
external
view
returns (
uint32 blockTimestamp,
int56 tickCumulative, // price accumulator
uint160 secondsPerLiquidityCumulativeX128,
bool initialized
);
The complete code can be found at this repository. First we query the original price accumulator from the pool and save it to a csv file
Function function = new Function("observations",
Arrays.asList(new Uint(BigInteger.valueOf(index))),
Arrays.asList(new TypeReference<Uint32>() { // blockTimestamp
},
new TypeReference<Int56>() { // tickCumulative
},
new TypeReference<Uint160>() { // secondsPerLiquidityCumulativeX128
},
new TypeReference<Bool>() { // initialized
}));
List<Type> rets = evmService.ethCall(null, contractAddr, function);
if (rets == null) return null;
int blockTimeStamp = ((BigInteger)rets.get(0).getValue()).intValue();
BigInteger tickCumulative = (BigInteger)rets.get(1).getValue();
BigInteger secondsPerLiquidityCumulativeX128 = (BigInteger)rets.get(2).getValue();
Boolean initialized = (Boolean)rets.get(3).getValue();
Then we read the data from the file and calculate the time-weighted average prices with different time periods.
for (int i = 1; i < beans.size(); i++) {
ObservationBean currentObservation = beans.get(i);
ObservationBean previousObservation = null;
int deltaSeconds = 0;
for (int j = i - 1; j >= 0; j--) {
previousObservation = beans.get(j);
deltaSeconds = currentObservation.getBlockTimeStamp() - previousObservation.getBlockTimeStamp();
if (deltaSeconds >= minPeriod) break;
}
if (deltaSeconds < minPeriod) continue;
BigInteger deltaTickCumulative = currentObservation.getTickCumulative().subtract(previousObservation.getTickCumulative())
.divide(BigInteger.valueOf(deltaSeconds));
BigDecimal base = new BigDecimal("1.0001");
BigDecimal price = null;
if (deltaTickCumulative.intValue() < 0) {
price = base.pow(-deltaTickCumulative.intValue());
price = BigDecimal.valueOf(1e12).divide(price, 2, RoundingMode.HALF_EVEN);
} else {
price = base.pow(deltaTickCumulative.intValue()).multiply(BigDecimal.valueOf(1e12));
}
}
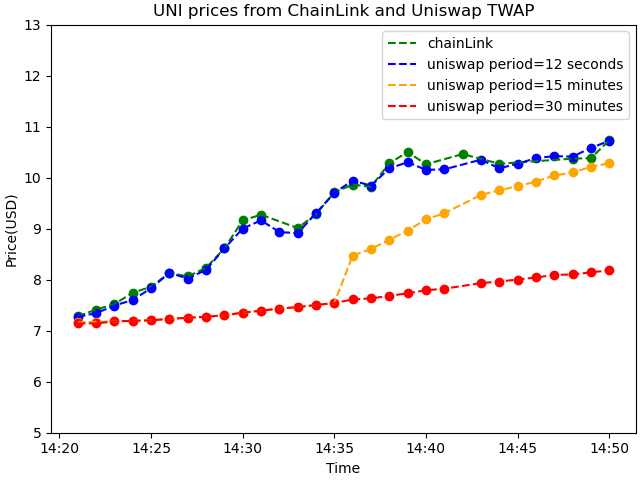
We can choose different periods for TWAP, the minimum 12 seconds, 900 seconds(15 minutes) and 1800 seconds(half an hour). The difference is obvious.

1 uniswap website 2 Uniswap v3 White Paper 3 Uniswap v3 core source code. IUniswapV3PoolState.sol
Written by Songziyu @China Apr. 2024